#NCS#인적성#필기#명제#어떤모든#필기시험#명제팁#결론고르기#명제쉽게푸는법#명제문제쉽게푸는방법삭제

안녕하세요!
취준도우미입니다.
이번 시간은 명제 문제를 쉽게 푸는 방법에 대해 설명해드리겠습니다.
명제는 쉽게 말해 참/거짓을 판별할 수 있는 문장이라고 이해하시면 됩니다.
예를들어 '짜장면은 5,000원이다.'라는 문장이 있다면 짜장면이 5,000원일 때 참이고 5,000원이 아닐 때 거짓이므로 참/거짓을 판별할 수 있는 문장이 되는 것이라 명제가 되는 것입니다.
개념은 참 쉽죠?
문제에서는 'A이면 B이다.' 와 같은 명제가 제시되어 출제되는 유형들은 다음과 같습니다. 어딜가나 똑같아요.
1. 전제가 주어지고 결론을 고르기
2. 전제가 1개 빼고 주어지고, 결론도 주어졌을 때 빈칸에 들어갈 전제 고르기
여기서 주의할 점은 문제를 푸실 때 별다른 언급이 없다면 전제는 무조건 참이라고 가정하고 푸셔야 합니다.
예를 들어 전제로 '여름의 기온은 영하이다.'라고 언급이 있다면 해당 문제에서는 여름의 기온은 영하가 되는 겁니다.
각자의 상식에 벗어났다하더라도 문제에 제시된 그대로 문제를 푸셔야 하는 점 참고하시면 됩니다.
문제 유형은 위의 두 가지로 출제된다 생각하시면 되지만 어려운 점은 '모든/어떤', '또한/그리고'에 대한 판단일 것입니다. 다들 이 부분에 어려움을 많이 느끼거든요. 그래서 오늘 이 부분에 대해 집중적으로 다뤄볼까 합니다.
기본 개념은 여기까지 설명하고 바로 문제를 풀면서 문제를 푸는 방법에 대해 설명드릴게요.
유형1. 전제가 주어지고 결론을 고르는 문제
1. 주어진 전제를 통해 도출되는 결론으로 항상 옳은 것을 고르면?
전제1: 밥을 먹은 어떤 사람은 디저트를 먹는다.
전제2: 밥을 먹은 모든 사람은 화장실을 간다.
결론:
① 밥을 먹지 않은 어떤 사람은 디저트를 먹지 않는다.
② 디저트를 먹은 어떤 사람은 화장실을 가지 않는다.
③ 화장실을 가는 모든 사람은 디저트를 먹는다.
④ 화장실에 가지 않으면서 밥을 먹는 사람이 있을 수 있다.
⑤ 화장실에 가는 어떤 사람은 디저트를 먹는다.
위의 문제 정답은 ⑤번 입니다.
이 문제는 전제가 주어지고 결론을 고르는 문제에 '모든/어떤'이 섞인 문제로 푸는 방법을 모르면 엄청 헷갈리고 오답을 고를 확률이 높습니다.
이 문제의 가장 쉬운 문제풀이법 소개해드릴게요.
1. 가장 먼저 벤다이어그램 3개를 겹쳐서 그려줍니다.

2-1. 전제의 내용을 토대로 적어도 1구간 존재하는 부분과 항상 없는 부분을 표시합니다. 밥을 먹은 모든 사람은 화장실을 가므로 밥 구간의 사람은 화장실을 가야 하므로 아래와 같은 그림이 나옵니다. 파란색으로 색칠된 부분은 해당 구간에 포함된 사람이 없음을 의미합니다.
* 저는 설명을 위해 파란색/빨간색으로 표시하지만 실제 문제를 풀때는 빗금이나 X표시, V표시 등 편한 방법으로 하시면 됩니다.
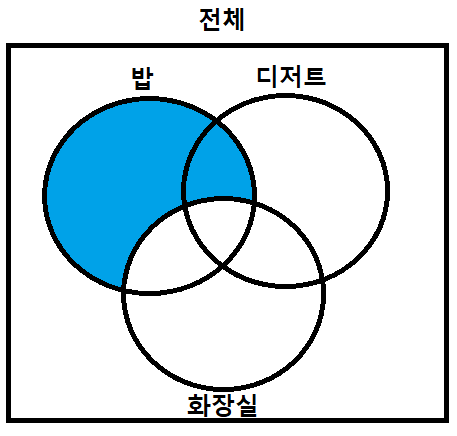
2-2. 밥을 먹은 어떤 사람은 디저트를 먹어야 하므로 밥 구간과 디저트 구간의 공통되는 음영은 무조건 적어도 1구간 존재해야 합니다. 무조건 존재하는 부분은 빨간색으로 표시해보면 아래와 같은 그림이 나옵니다.

3. 전제를 통해 벤다이어그램을 완성했다면 이제 선택지 소거를 하면 됩니다. 이때 주의해야 할 점은 하얀색 구간은 있는지 없는지 100% 확답할 수 없습니다.
주의할 점을 생각하며 파란색, 빨간색, 하얀색 구간에 해당되는 선택지를 보고 적절하게 판단해주면 됩니다.
오답을 어떻게 소거하는지 살펴보겠습니다.
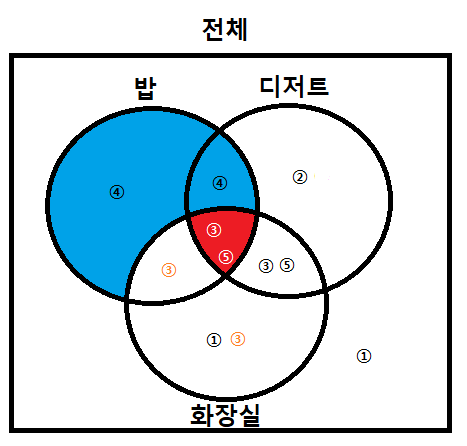
① 밥을 먹지 않은 어떤 사람은 디저트를 먹지 않는다.
그림의 ①부분이 ①선택지가 나타내는 부분이 됩니다. 이 부분은 둘 다 모두 하얀색으로 표시되어있기 때문에 둘 다 없을 경우가 존재할 수 있어 오답이 됩니다.
② 디저트를 먹은 어떤 사람은 화장실을 가지 않는다.
그림의 ②부분이 ②선택지가 나타내는 부분이 됩니다. 이 부분 또한 하얀색으로 표시되어 있을 수도 있고 없을 수도 있으므로 항상 옳다고 볼 수 없으므로 오답이 됩니다.
③ 화장실을 가는 모든 사람은 디저트를 먹는다.
화장실을 가는 모든 사람은 디저트를 먹는다고 하였으므로 주황색으로 표시된 ③에 사람이 없어야 하고 화장실과 디저트구간이 겹치는 곳에만 사람이 존재해야 합니다. 일단. 빨간색 부분은 항상 존재하는 부분이므로 참이 될 수 있다고 생각할 수 있지만, 주황색으로 표시된 ③은 사람이 있는지 없는지 알 수 없으므로 항상 옳다고 볼 수 없기에 오답이 됩니다.
만약 화장실을 가는 어떤 사람은 디저트를 먹는다고 했으면 빨간색 부분은 항상 존재하기 때문에 정답으로 될 수 있겠지만 해당 문제는 ‘어떤’이 아닌 ‘모든’이므로 오답이 됩니다.
④ 화장실에 가지 않으면서 밥을 먹는 사람이 있을 수 있다.
화장실에 가지 않으면서 밥을 먹는 사람은 그림의 ④에 해당하는 부분이지만 파란색으로 표시된 부분은 사람이 존재하지 않으므로 거짓이 되므로 오답이 됩니다.
⑤ 화장실에 가는 어떤 사람은 디저트를 먹는다.
화장실에 가는 어떤 사람은 디저트를 먹으므로 화장실과 디저트 구간의 겹친 부분인 그림에서 ⑤표시된 구간 중 1구간 이상 확실히 존재하면 참이 되는데 빨간색 구간은 반드시 존재하는 구간이므로 ⑤가 정답이 됩니다.
같은 유형의 문제를 다시 실습해 보도록 하겠습니다. 1번 문제에서는 빨간색 구간이 확정되어있어 쉬운 문제였다면 이번 문제는 난이도를 조금 올려서 풀어보도록 하겠습니다.
유형1. 전제가 주어지고 결론을 고르는 문제
1. 주어진 전제를 통해 도출되는 결론으로 항상 옳은 것을 고르면?
전제1: 우유를 먹는 어떤 사람은 키가 크다.
전제2: 운동을 하는 모든 사람은 우유를 먹는다.
결론:
① 운동을 하는 모든 사람은 키가 크지 않다.
② 키가 크지 않은 어떤 사람은 운동을 한다.
③ 운동을 하지 않는 어떤 사람은 키가 크다.
④ 우유를 먹지 않는 어떤 사람은 운동을 한다.
⑤ 키가 큰 어떤 사람은 우유를 먹는다.
위의 문제의 정답은 ⑤번 입니다. 이 문제도 바로 위 문제와 똑같이 풀어보겠습니다.
1. 가장 먼저 벤다이어그램 3개를 겹쳐서 그려줍니다.

2-1. 전제의 내용을 토대로 적어도 1구간 존재하는 부분과 항상 없는 부분을 표시합니다. 먼저 '운동을 하는 모든 사람은 우유를 먹는다.'의 전제로 얻을 수 있는 부분을 표시하겠습니다. 운동을 하는 모든 사람이 우유를 먹어야 하므로 운동을 하는 사람 중 우유를 먹지 않는 사람의 구간을 제거한 형태입니다.

2-2 '우유를 먹는 어떤 사람은 키가 크다.'의 전제로 얻을 수 있는 부분을 표시하겠습니다. 1번 문제와 다르게 이번 문제에는 빨간색 구간이 2개 구간 나타난 것을 볼 수 있습니다. 이 의미는 '두 두간 모두 반드시 존재한다'가 아닌 '두 구간 중 적어도 한개 구간은 존재한다'는 의미입니다. (너무나도 중요하여 배경색 표시 함)

3. 전제를 통해 벤다이어그램을 완성했다면 이제 선택지 소거를 하겠습니다. 이때도 주의할 점은 하얀색 구간은 존재하는지 존재하지 않는지 확실히 판단할 수 없다는 것입니다.

① 운동을 하는 모든 사람은 키가 크지 않다.
그림의 ①이 포함된 구간은 하얀색 구간과 빨간색 구간입니다. 운동을 하는 모든 사람은 키가 크지 않아야 하지만 빨간색 구간 2개 중 1개의 구간은 무조건 존재해야 하므로 ①이 포함된 빨간색 구간이 존재할 경우가 있을 수 있으므로 항상 옳지 않기 때문에 오답이 됩니다.
② 키가 크지 않은 어떤 사람은 운동을 한다.
키가 크지 않은 어떤 사람은 운동을 해야 하므로 그림의 ②가 포함된 구간은 하얀색 구간이므로 존재하는지 존재하지 않는지 확실하지 않기 때문에 항상 옳은 결론이 될 수 없습니다. 따라서 ②선택지도 오답이 됩니다.
③ 운동을 하지 않는 어떤 사람은 키가 크다.
운동을 하지 않는 어떤 사람은 키가 크다는 것은 그림의 검정색 ③이 포함된 구간 중 적어도 1개 구간이 존재해야 한다는 것을 의미합니다. 하얀색 구간은 있는지 없는지 확실하지 않고, 빨간색 구간 중 노란색 ③이 포함된 구간이 존재할 경우 검정색 ③이 포함된 구간은 존재하지 않을 수도 있어 검정색 ③이 포함된 구간 모두 존재하지 않을 수 있습니다. 따라서 항상 옳은 결론이 아니므로 오답이 됩니다.
④ 우유를 먹지 않는 어떤 사람은 운동을 한다.
우유를 먹지 않는 어떤 사람은 운동을 한다는 것은 그림의 ④가 포함된 구간입니다. 해당 구간은 모두 파란색 구간이므로 절대 존재할 수 없기 때문에 항상 거짓인 결론이므로 오답이 됩니다.
⑤ 키가 큰 어떤 사람은 우유를 먹는다.
'키가 큰 어떤 사람은 우유를 먹는다'는 그림의 ⑤가 포함된 구간 중 적어도 1개 구간 존재하면 정답이 됩니다. ⑤가 포함된 구간은 둘 다 빨간색 구간으로 해당 구간 중 적어도 1개 구간은 무조건 존재해야하기 때문에 항상 옳은 결론이 되어 ⑤번이 정답이 됩니다.
제가 정말 많은 문제를 풀어보고 다양한 강의를 들어본 결과 가장 효율적인 문제 풀이 방법인 것 같습니다.
이번 시간은 명제 중 결론을 고르는 문제를 풀어봤는데 혹여 이해가 안가시는 부분이 있으시다면 댓글로 질문 남겨주신다면 확인 후 답변 드리도록 하겠습니다.
다음 글에는 2. 전제가 1개 빼고 주어지고, 결론도 주어졌을 때 빈칸에 들어갈 전제 고르기 [쉽게 전제 고르는 문제]를 쉽게 푸는 방법을 공유 드리겠습니다.
오늘 콘텐츠가 취준생 여러분께 도움이 많이 됐으면 좋겠고 글이 좋았다고 생각되시면 하트..댓글..달아주시면 저에게 큰 힘이 됩니다.!
'NCS' 카테고리의 다른 글
| 명제 문제 쉽게 풀기 2편(어떤이 포함되지 않은 명제) (0) | 2020.05.18 |
|---|

